2025-05-30

Innovation Highlights
张景昭—提出“懒”外插牛顿法 (Lazy Extra Newton method,简称为LEN),并且证明该算法可以突破“最优”算法的计算复杂度。例如,当使用经典的矩阵求逆算法实现牛顿步的时候,团队的算法对于d维优化问题可以得到d^(1/3) 因子的加速。并且,团队使用重启动技术将算法推广到强凸-强凹问题上,得到类似的计算复杂度上的改进。
Achievements Summary
机器人操作模仿学习的数据扩展定律
凸-凹极小极大问题(又被称为鞍点计算问题)是优化中的基础问题。Monteiro 和Svaiter 在2012年就已经提出了该问题关于Oracle(函数的梯度以及Hessian矩阵)调用次数的最优算法。然而,人们并不知道Monteiro 和Svaiter的算法是否在计算复杂度上也是最优的。
课题组成功将Doikov et al. (ICML 2023) 基于极小化问题提出的“懒”Hessian技术应用到凸-凹极小极大优化问题,并且得到了突破已知关于Oracle调用次数“最优”算法的计算复杂度。文章的创新点在于将“懒”Hessian技术以及外插梯度法(extra-gradient)的分析相结合,并且处理两种技术结合中产生的额外误差。对于算法中所需要的极小极大三次正则牛顿法子问题的求解,文章也提出了高效的求解器,克服极小极大问题中Hessian矩阵非正定带来的困难。
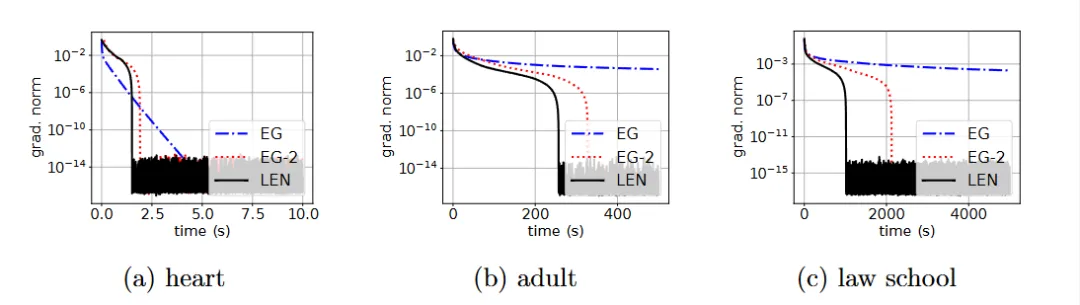
图. 在真实数据集上的实验

图. 本文提出的“懒”外插牛顿法的迭代格式
该工作使用的外插牛顿的框架,具有更广的适用性。在该工作的拓展版本(https://arxiv.org/abs/2501.17488)中,该课题组也成功结合动量加速将该框架运用到了极小化问题中,进而得到了在凸优化中突破“最优”算法计算复杂度的结果。
该成果被选为ICLR 2025的Oral论文。本成果共同一作为上海期智研究院实习生、清华大学博士生陈乐偲,香港中文大学博士生刘程畅,通讯作者为上海期智研究院PI、清华大学助理教授张景昭。
论文信息:
Second-Order Min-Max Optimization with Lazy Hessians, Lesi Chen*, Chengchang Liu*, Jingzhao Zhang†, https://arxiv.org/pdf/2410.09568, ICLR 2025.