上海期智研究院PI,清华大学交叉信息研究院助理教授。
本科毕业于UC Berkeley,博士毕业于MIT计算机科学系 (EECS)。他的研究致力于为实用算法提供简洁而具预测性的理论分析,同时关注空间受限算法的计算复杂性理解。他曾获MIT人工智能和决策领域最佳硕士论文奖、最佳博士论文奖,入选2022年度国家海外人才计划,指导学生获国际学习理论会议 (COLT) 最佳学生论文奖。
个人荣誉
IIIS青年学者奖学金
麻省理工学院最佳人工智能和决策硕士论文
麻省理工学院最佳人工智能和决策博士论文
伯克利研究生奖学金
麻省理工学院Lim研究生奖学金
机器学习理论:计算问题的信息、样本复杂度上下界
深度学习:神经网络的训练简化、理解和加速
动力系统:动力系统在强化学习和电池领域的应用
成果12:数据混合下大模型知识学习的相变规律(2025年度)
张景昭团队提出,大模型在混合数据上预训练时,从知识密集型数据中获取知识并非“模型越大、配比越高就越好”,而是在模型规模和知识数据占比上存在类似“相变”的现象:当模型容量或混合比例低于阈值时,即便每条知识被看到上百次,模型几乎无法记住任何事实;一旦超过阈值,记忆量会从接近零突然跃迁到掌握大部分知识。论文通过信息论建模为该现象提供了理论解释:有限容量模型在不同数据集之间必须进行类似“背包问题”的容量分配,因而最优策略会随模型规模或混合比例变化而离散跳变。该理论分析进一步给出“临界混合比例与模型大小满足幂律关系“的推论。本文揭示了“大模型的好配方未必适用于小模型、反之亦然”, 对实际大模型训练的数据配比选择有指导意义。
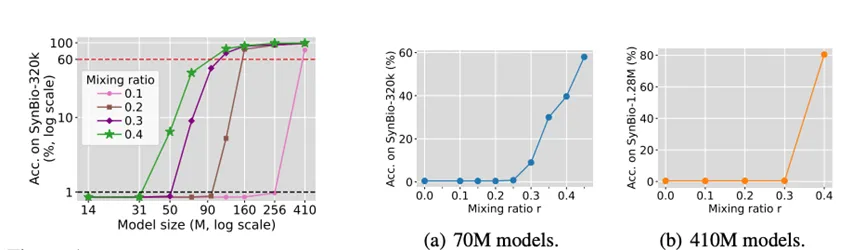
图. 模型知识学习效果关于模型大小和知识数据混合比例的相变现象
论文信息:
https://arxiv.org/abs/2505.18091
Data Mixing Can Induce Phase Transitions in Knowledge Acquisition, Xinran Gu*, Kaifeng Lyu*, Jiazheng Li, Jingzhao Zhang†,NeurIPS 2025 Spotlight.
------------------------------------------------------------------------------------------------------------------------------
成果11:有限采样下的连续时间线性系统的分析:系统识别和在线控制问题(2025年度)
张景昭团队提出连续时间线性系统的系统识别算法。该算法利用等间隔采样下的数据符合离散线性演化的性质,通过这些数据首先估计离散线性系统的参数。当数据采样频率高于某一常数(只与原始系统相关)时,可对估计的离散参数进行泰勒展开等解析运算,恢复出连续系统的参数,且误差只与总运行时间有关![]() 并达到最优。这突破了传统方法中需要不断提高采样频率才能减小估计误差的局限性,保证了随时间线性的计算开销下能够完成任意精度的参数估计,并能够在下游任务,如在线控制中达到优于已有算法的效果。
并达到最优。这突破了传统方法中需要不断提高采样频率才能减小估计误差的局限性,保证了随时间线性的计算开销下能够完成任意精度的参数估计,并能够在下游任务,如在线控制中达到优于已有算法的效果。
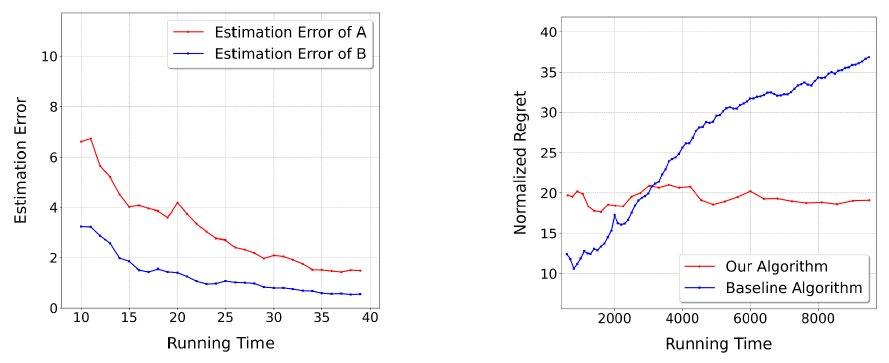
图. 算法得到了实证验证
论文信息:
https://arxiv.org/pdf/2509.22741
Finite Sample Analyses for Continuous-time Linear Systems: System Identification and Online Control, Hongyi Zhou*, Jingwei Li*, Jingzhao Zhang†,NeurIPS 2025.
------------------------------------------------------------------------------------------------------------------------------
成果10:理解非线性神经网络隐式偏差:基于输入空间的区域计数(2025年度)
张景昭团队提出了通过输入空间中预测标签相同的连通区域数量(决策区域数)来刻画隐式偏差。相比依赖参数的指标,决策区域数更适用于非线性神经网络的刻画,因为它具有重参数化不变性。实验表明,较小的区域数对应几何简单的决策边界,并与良好泛化性能显著相关;较大的学习率和较小的批次规模等超参数选择会减少区域数。
论文信息:
https://arxiv.org/pdf/2505.11370
Understanding Nonlinear Implicit Bias via Region Counts in Input Space, Jingwei Li*, Jing Xu*, Zifan Wang, Huishuai Zhang, Jingzhao Zhang†, ICML 2025.
------------------------------------------------------------------------------------------------------------------------------
成果9:面向黑盒的扩散模型成员推理攻击研究(2025年度)
张景昭团队提出一种仅需调用图像变换API、无需访问U-net的新型成员推断攻击方法。该方法基于关键发现:模型对训练集图像能更稳定地获得无偏噪声预测估计。通过对目标图像多次调用API、平均输出结果并与原图比对,该方法可有效判定样本是否属于训练集。团队在DDIM和Stable Diffusion框架上验证了方法的有效性,并将本方法与之前算法拓展至Diffusion Transformer架构。
论文信息:
https://arxiv.org/pdf/2405.20771
Towards Black-Box Membership Inference Attack for Diffusion Models, Jingwei Li, Jing Dong, Tianxing He, Jingzhao Zhang†, ICML 2025.
------------------------------------------------------------------------------------------------------------------------------
成果8:基于逐层蒸馏的可扩展模型融合方法(2025年度)
张景昭团队提出了一种新方法 ProDistill(逐层蒸馏),将模型融合问题视作知识蒸馏过程,按层进行训练,以减少内存开销并提升融合效果。实验证明,该方法在视觉和自然语言任务中相比现有方法最高提升 6.14% 和 6.61%,并首次将训练型融合方法成功扩展到百亿参数级别的大模型融合任务。
论文信息:
https://arxiv.org/pdf/2502.12706
Scalable Model Merging with Progressive Layer-wise Distillation, Jing Xu, Jiazheng Li, Jingzhao Zhang†, ICML 2025.
------------------------------------------------------------------------------------------------------------------------------
成果7:从依赖关系的稀疏性到注意力模式的稀疏性:揭示思维链如何提高Transformer的样本效率(2025年度)
思维链(CoT)能显著提升大语言模型(LLM)的推理能力。当前的理论研究通常将这一提升归因于模型的表达能力和计算能力的增强。然而,即使在简单任务上,大模型仍可能出现失误,因此团队认为,在大模型的语境下,表达能力并非主要的限制因素。
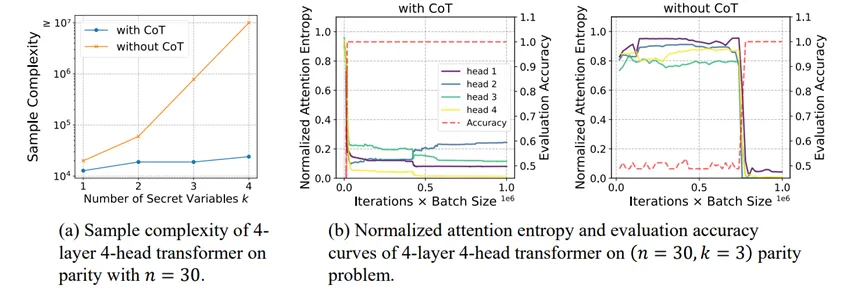
图. (1)使用CoT可以显著提高样本效率。(b)当注意力层变得更加稀疏,准确率都会出现显著提升。
思维链(CoT)通过将复杂任务分解为简单、可操作的子步骤,显著提升了模型的推理能力。显著提升了模型的推理能力。为了深入探究思维链成功背后的机制,张景昭课题组以sparse parity这一简单问题为切入点,证明了思维链能够以指数级降低Transformer模型的样本复杂度。
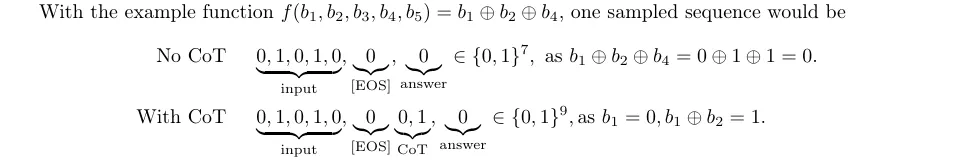
图. 在无/有CoT时的问题和数据格式
具体来说,项目组成员从理论上证明了:
(1)表达能力充足:即使在没有思维链的情况下,仅需一层、单头的Transformer模型即可表达sparse parity问题。
(2)无思维链时的困难性:在没有思维链时,Transformer模型需要指数多的样本复杂度,才能得到非平凡的准确率。
(3)思维链能降低模型的样本复杂度:当使用带有思维链的数据进行训练时,Transformer模型只需要接近线性的样本复杂度,即可在sparse parity问题上达到完美的准确率。
此外,由于思维链分解了token之间的依赖关系,Transformer的注意力层在该问题上呈现稀疏且可解释的特征。
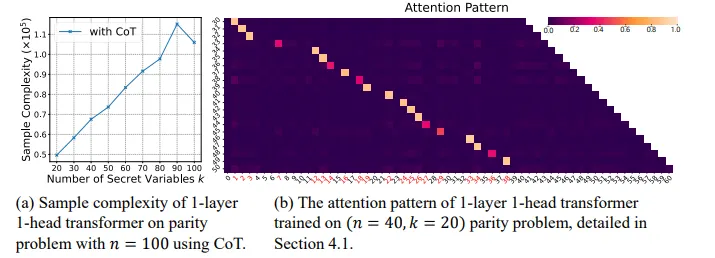
图. (a)对于固定的n,使用思维链学习sparse parity问题的样本复杂度大致随k线性增长。(b)使用思维链时,Transformer学到的注意力模式具有可解释性。
这一简化模型的结论在真实场景中得到了验证:与无CoT的数据相比,预训练模型在有CoT数据上展现出更稀疏的注意力模式;而通过CoT数据微调,可以进一步增强注意力的稀疏性。
------------------------------------------------------------------------------------------------------------------------------
成果6:基于“懒”Hessian技术的极小极大问题二阶优化(2025年度)
凸-凹极小极大问题(又被称为鞍点计算问题)是优化中的基础问题。Monteiro 和Svaiter 在2012年就已经提出了该问题关于Oracle(函数的梯度以及Hessian矩阵)调用次数的最优算法。然而,人们并不知道Monteiro 和Svaiter的算法是否在计算复杂度上也是最优的。
课题组成功将Doikov et al. (ICML 2023) 基于极小化问题提出的“懒”Hessian技术应用到凸-凹极小极大优化问题,并且得到了突破已知关于Oracle调用次数“最优”算法的计算复杂度。文章的创新点在于将“懒”Hessian技术以及外插梯度法(extra-gradient)的分析相结合,并且处理两种技术结合中产生的额外误差。对于算法中所需要的极小极大三次正则牛顿法子问题的求解,文章也提出了高效的求解器,克服极小极大问题中Hessian矩阵非正定带来的困难。
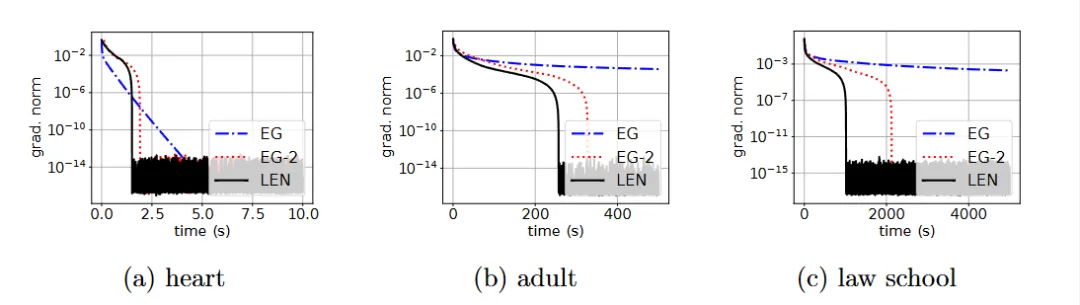
图. 在真实数据集上的实验

图. 本文提出的“懒”外插牛顿法的迭代格式
该工作使用的外插牛顿的框架,具有更广的适用性。在该工作的拓展版本(https://arxiv.org/abs/2501.17488)中,该课题组也成功结合动量加速将该框架运用到了极小化问题中,进而得到了在凸优化中突破“最优”算法计算复杂度的结果。
------------------------------------------------------------------------------------------------------------------------------
成果5:智能体生成器:一种通过行为提示扩散生成通用策略网络的框架(2024年度)


图1. FC-BiO算法流程
团队在真实数据集上评估FC-BiO与已有方法的表现。结果显示, FC-BiO的求解效果显著优于已有方法,与理论结果一致。
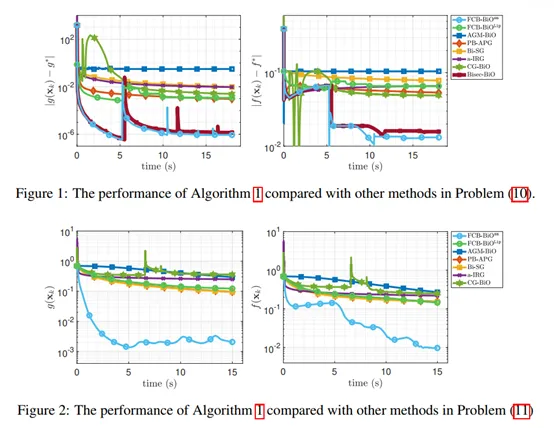
图2. FC-BiO的求解效果显著优于其他已有算法
本工作弥合了一阶优化算法求解简单双层凸优化问题复杂度下界和上界的差距。
论文信息:Functionally Constrained Algorithm Solves Convex Simple Bilevel Problems, Huaqing Zhang*, Lesi Chen*, Jing Xu, Jingzhao Zhang†, https://arxiv.org/abs/2409.06530, NeurIPS 2024.
------------------------------------------------------------------------------------------------------------------------------
成果4:基于随机掩码的参数高效微调(2024年度)
微调是提升大型语言能力与安全性的重要步骤。参数高效微调通过减少参数训练量,大幅降低了微调的开销。针对特定任务进行参数微调是提高预训练模型性能的关键步骤。参数高效微调 (parameter efficient fine-tuning, PEFT) 通过在大模型中增加可训练轻量级模块,能显著降低微调算法的显存开销。为了探究参数高效微调算法的设计原理与性能极限,张景昭课题组研究了一种参数高效微调方法: 随机掩码 (Random Masking)。
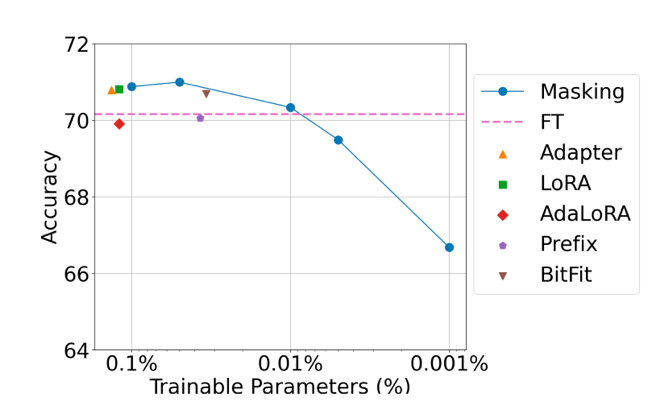
图3. 参数高效算法的性能与可训练参数量的关系。
Masking为本文提出的随机掩码算法
随机掩码相较于现有的标准参数高效微调算法,例如LoRA,具有算法设计简单、训练参数量更少等特点。团队成员通过大规模实验发现,适当的学习率选择对随机掩码的成功至关重要,只需使用较大的学习率,随机掩码算法能在一些任务中取得与标准参数高效微调方法相当的性能。
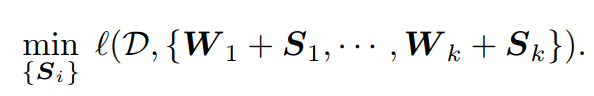
图4. 随机掩码算法的数学表示

图5. 掩码方法示意图。红色网格表示可训练的参数,蓝色网格表示被冻结的参数
团队成员对该现象给出了理论与实验分析,证明了随机掩码的出色性能得益于大语言模型强大的表达能力,以及掩码使损失函数更平滑,降低了优化难度。该论文提出的随机掩码算法不仅为参数高效微调方法的设计与分析提供了新思路,而且对降低大规模预训练模型的微调成本具有重要实际价值。相关成功收录于ICML 2024中。本论文一作为清华大学交叉信息研究院博士生许靖。
论文信息:Random Masking Finds Winning Tickets for Parameter Efficient Fine-tuning, Jing Xu, Jingzhao Zhang, http://arxiv.org/abs/2405.02596, ICML 2024.
------------------------------------------------------------------------------------------------------------------------------
成果3:通过动态深度学习实现锂离子电池的真实故障检测(2024年度)
张景昭团队研究了分布式深度学习中的数据并行训练问题, 提出了Quadratic Synchronization Rule(QSR)的新方法,不仅考虑了通信成本和优化速度之间的权衡,而且还考虑了同步周期H对模型泛化能力的影响,在减少通信量和提高测试准确率方面的显著效果。
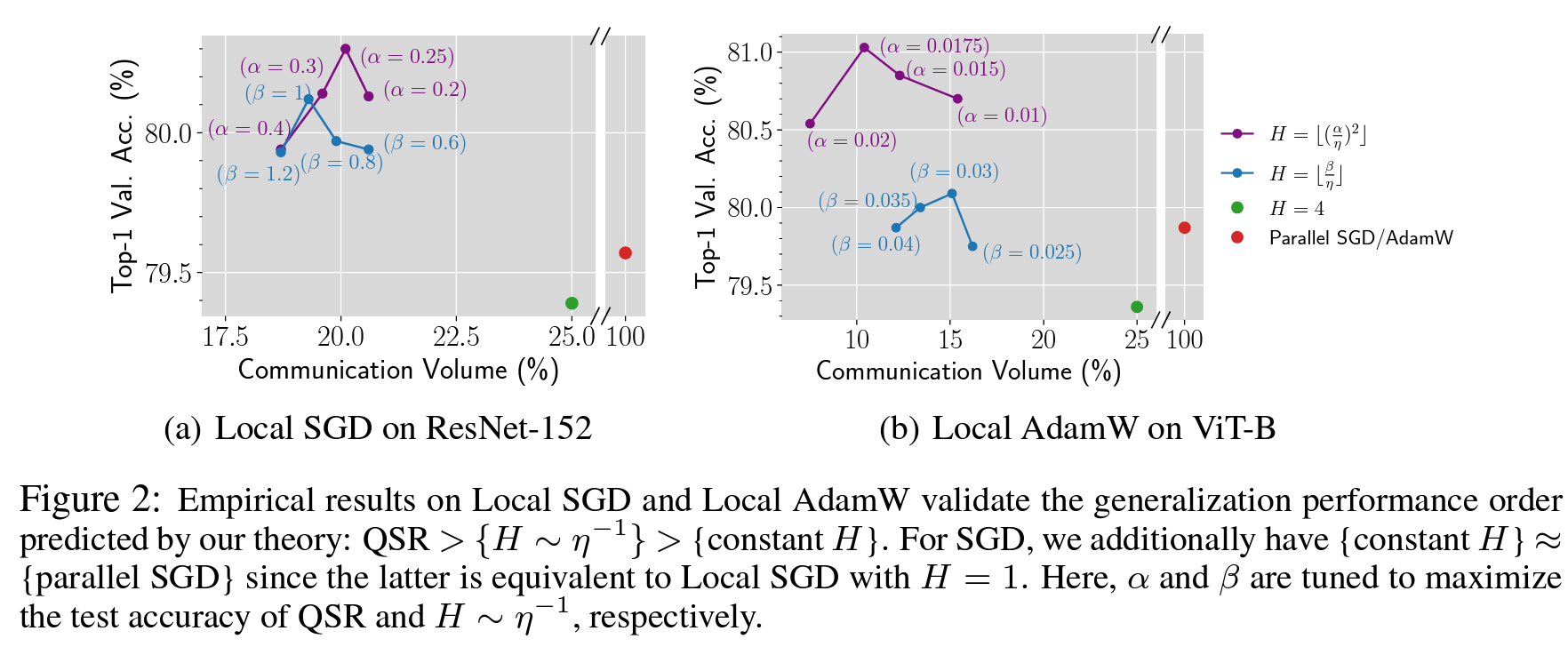
论文信息:A Quadratic Synchronization Rule for Distributed Deep Learning,Xinran Gu*, Kaifeng Lyu*, Sanjeev Arora, Jingzhao Zhang, Longbo Huang,https://github.com/hmgxr128/QSR
------------------------------------------------------------------------------------------------------------------------------
成果2:通过动态深度学习实现锂离子电池的真实故障检测(2023年度)
准确评估锂离子电池(LiB)安全状况可以减少意外电池故障,促进电池部署并促进低碳经济。尽管人工智能最近取得了进展,但由于复杂的故障机制以及缺乏具有大规模数据集的真实测试框架,异常检测方法并未针对实际电池设置进行定制或验证。在这里,我们开发了一个用于电动汽车 (EV) LiB 异常检测的现实深度学习框架。它具有专为动态系统量身定制的动态自动编码器,并根据社会和财务因素进行配置。我们在已发布的数据集上测试了我们的检测算法,该数据集包含 347 辆电动汽车的 690,000 多个 LiB 充电片段。我们的模型克服了最先进的故障检测模型(包括深度学习模型)的局限性。此外,它还减少了预期的电动汽车电池直接故障。
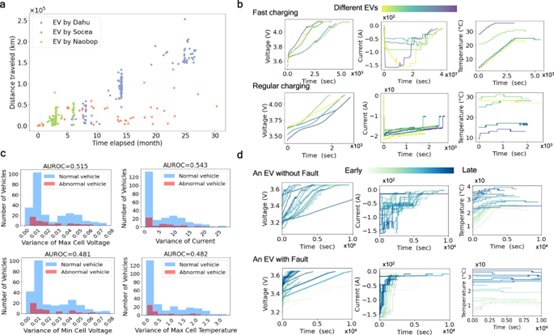
研究论文:Zhang, Jingzhao, et al. "Realistic fault detection of li-ion battery via dynamical deep learning." Nature Communications 14.1 (2023): 5940.
论文链接:https://people.csail.mit.edu/yichenl/projects/preconditioner/
------------------------------------------------------------------------------------------------------------------------------
成果1:测地度量空间中的 Sion 极小极大定理和黎曼外梯度算法(2023年度)
对于非凸非凹问题,确定鞍点是否存在或是否可近似通常很棘手。本文朝着理解一类仍然易于处理的非凸非凹极小极大问题迈出了一步。具体来说,它研究测地度量空间上的极小极大问题,这提供了通常的凸凹鞍点问题的广泛概括。论文的第一个主要结果是 Sion 极小极大定理的测地度量空间版本;我们相信我们的证明是新颖的并且可以广泛使用,因为它仅依赖于有限交集属性。第二个主要结果是测地完整黎曼流形的专门化:在这里,我们设计并分析了平滑极小极大问题的一阶方法的复杂性。

研究论文:Zhang, Peiyuan, Jingzhao Zhang, and Suvrit Sra. "Sion’s Minimax Theorem in Geodesic Metric Spaces and a Riemannian Extragradient Algorithm." SIAM Journal on Optimization 33.4 (2023): 2885-2908.
13. Understanding Nonlinear Implicit Bias via Region Counts in Input Space, Jingwei Li*, Jing Xu*, Zifan Wang, Huishuai Zhang, Jingzhao Zhang†, ICML 2025.
12. Towards Black-Box Membership Inference Attack for Diffusion Models, Jingwei Li, Jing Dong, Tianxing He, Jingzhao Zhang†, ICML 2025.
11. Scalable Model Merging with Progressive Layer-wise Distillation, Jing Xu, Jiazheng Li, Jingzhao Zhang†, ICML 2025.
10. Finite Sample Analyses for Continuous-time Linear Systems: System Identification and Online Control, Hongyi Zhou*, Jingwei Li*, Jingzhao Zhang†,NeurIPS 2025.
9. Data Mixing Can Induce Phase Transitions in Knowledge Acquisition, Xinran Gu*, Kaifeng Lyu*, Jiazheng Li, Jingzhao Zhang†,NeurIPS 2025 Spotlight.
8. Online Control with Adversarial Disturbance for Continuous-time Linear Systems, Jingwei Li, Jing Dong, Can Chang, Baoxiang Wang, Jingzhao Zhang†, https://arxiv.org/pdf/2306.01952, NeurIPS 2024.
7. Functionally Constrained Algorithm Solves Convex Simple Bilevel Problems, Huaqing Zhang*, Lesi Chen*, Jing Xu, Jingzhao Zhang†, https://arxiv.org/abs/2409.06530, NeurIPS 2024.
6. Random Masking Finds Winning Tickets for Parameter Efficient Fine-tuning, Jing Xu, Jingzhao Zhang, http://arxiv.org/abs/2405.02596, ICML 2024.
5. Xinran Gu*, Kaifeng Lyu*, Sanjeev Arora, Jingzhao Zhang, Longbo Huang, A Quadratic Synchronization Rule for Distributed Deep Learning, ICLR 2024
4. Zhang J, Wang Y, Jiang B, He H, Huang S, Wang C, Zhang Y, Han X, Guo D, He G, Ouyang M, Realistic fault detection of li-ion battery via dynamical deep learning, Nature Communications, 2023 查看PDF
3. Zhang, Peiyuan and Zhang, Jingzhao and Sra, Suvrit, Sion’s Minimax Theorem in Geodesic Metric Spaces and a Riemannian Extragradient Algorithm, SIAM Journal on Optimization, 2023 查看PDF
2. Cheng, X., Wang, B., Zhang, J., & Zhu, Y. , Fast Conditional Mixing of MCMC Algorithms for Non-log-concave Distributions, Conference on Neural Information Processing Systems (NeurIPS), 2023 查看PDF
1. Kaiyue Wen, Jiaye Teng, Jingzhao Zhang, Benign Overfitting in Classification: Provably Counter Label Noise with Larger Models, International Conference on Learning Representation (ICLR), 2023 查看PDF